Notes on Power Functions
Introduction
Bitmaps, be they single channel greyscale or RGB are essentially an array of values where each value is between 0 and 1.
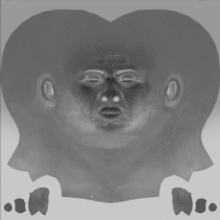
Greyscale Head Roughness Map
In a shader, when we use a parameter such as ‘Roughness Power’, this parameter is used in an operation which takes a value from the bitmap and raises it to the power of the parameter
i.e.
(here
is referred to as the base and
as the exponent. This operation is usually referred to as Exponentiation or a Power Law.
Blender uses the Math->Power ‘Converter’ type shadernode (light blue) to do this (shown below for illustration).
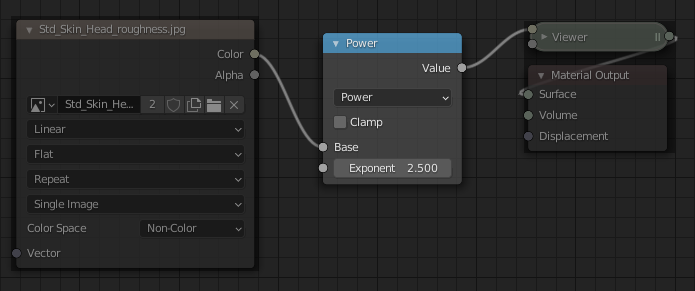
Converter Node: Math (Power)
This type of operation is known as Gamma Correction where ‘gamma’ () is the exponent,
is the base (i.e. the input bitmap) and
is a constant of proportionality which gives Gamma Corrected
(i.e. the output bitmap) in the expression:
Exponent Effects
When the base value you are raising to a power is between 0 and 1 (as is the case with a bitmap), the result can never be lower then 0 or greater than 1. Thus all the values in a bitmap can be safely tuned in a non-linear manner by only varying the exponent.
Important
The value of the exponent can have a dramatic effect on the bitmap. Consider the examples below:
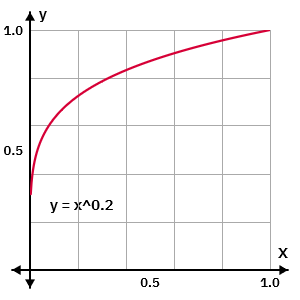
When the exponent is 0.2 ( i.e. the quintic root
) smaller values are amplified much more than the higher values (with a roughness map, this would mean that the smoother areas are made somewhat rougher; with a RGB image, the darker areas would be significantly lightened)
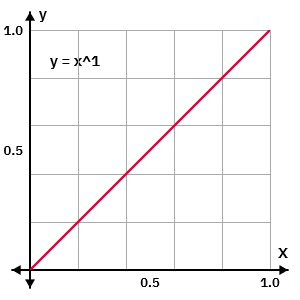
When the exponent is 1 (
) this is the neutral case where the operation makes no changes to the bitmap.
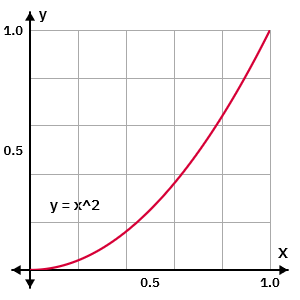
When the exponent is above 1 but still small, we can see a slight reduction in lower end values and a slight increase in higher end values e.g with .
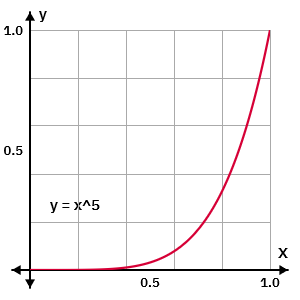
As the exponent becomes higher (e.g with ) we observe a very significant reduction of all but the highest end values (with a roughness map this would smooth out all but the roughest areas; with a RGB image, the lighter areas would be significantly darkened)
The value of the exponent should therefore be adjusted carefully.